Натуральный логарифм

Натуральный логарифм — это логарифм по основанию e, где e — это математическая константа, примерно равная 2.71828. Он обозначается как ln(x), где x — положительное число.

Почему именно e?

Константа e имеет множество удивительных свойств. Например, она возникает в различных областях, таких как:

• Экспоненциальный рост (например, популяции или инвестиции)


• Процесс радиоактивного распада


• Математический анализ и теория вероятностей

Формулы и свойства натурального логарифма

Вот несколько ключевых свойств натурального логарифма:

• ln(1) = 0: Логарифм единицы всегда равен нулю.


• ln(e) = 1: Логарифм числа e равен единице.


• ln(xy) = ln(x) + ln(y): Логарифм произведения равен сумме логарифмов.


• ln(x/y) = ln(x) - ln(y): Логарифм частного равен разности логарифмов.


• ln(x^k) = k * ln(x): Логарифм степени равен произведению степени на логарифм основания.

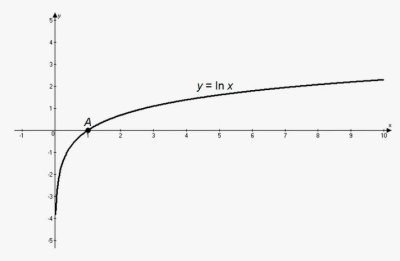
График натурального логарифма

График функции y = ln(x) выглядит следующим образом:

Применение натурального логарифма

Натуральный логарифм находит применение в различных областях:

• Экономика: Используется для расчета сложных процентов и анализа роста инвестиций.


• Физика: Применяется в формулах для описания процессов распада и роста.


• Информатика: Используется в алгоритмах и теории информации.

Примеры вычислений

Давай рассмотрим несколько примеров:

• ln(10) ≈ 2.302: Это означает, что e в степени 2.302 приближенно равно 10.


• ln(100) ≈ 4.605: e в степени 4.605 приближенно равно 100.

Заключение

Натуральный логарифм — это мощный инструмент, который помогает нам понимать и анализировать множество процессов в окружающем мире. Он не только математическая концепция, но и ключ к разгадке многих тайн природы!

Если у тебя есть вопросы или ты хочешь узнать больше о какой-то конкретной теме, не стесняйся спрашивать!