Асимптотическое поведение

Давай поговорим об асимптотическом поведении. Звучит сложно, но на самом деле это довольно просто. Если ты когда-нибудь задумывался о том, как ведет себя функция, когда её аргумент стремится к бесконечности, то ты уже на полпути к пониманию асимптотики. Это как наблюдать за тем, как ты идёшь по улице и приближаешься к своему любимому кафе — чем ближе ты подходишь, тем более предсказуемо становится твое поведение!

Что такое асимптота?

Представь себе, что у тебя есть функция, скажем, f(x) = 1/x. Когда x становится очень большим, f(x) стремится к нулю. Мы говорим, что y = 0 — это асимптота функции. То есть, чем дальше ты идешь по оси x, тем ближе функция подходит к оси x, но никогда её не пересекает. Это как если бы ты пытался дотянуться до своей любимой пиццы в холодильнике, но каждый раз, когда ты к ней приближаешься, она оказывается чуть дальше!

Типы асимптот

Есть несколько типов асимптот, и они все имеют свои особенности:

• Горизонтальная асимптота: Как уже упоминалось, это линия, к которой функция стремится при x → ∞. Пример: f(x) = 1/x.


• Вертикальная асимптота: Это линия, к которой функция стремится при стремлении аргумента к некоторому значению. Например, в функции f(x) = 1/(x-1), когда x → 1, функция стремится к бесконечности.


• Наклонная асимптота: Это линия, которая описывает поведение функции на бесконечности. Например, для функции f(x) = 2x + 3, наклонная асимптота будет y = 2x.

Применение асимптотики

Теперь давай поговорим о том, зачем нам вообще нужна асимптотика. Это как если бы ты был шеф-поваром и хотел знать, как долго готовить пасту. Асимптотический анализ позволяет нам понять поведение алгоритмов при больших входных данных. Например, если у тебя есть алгоритм сортировки с временной сложностью O(n^2), то при увеличении объема данных его время выполнения будет расти в квадрате! Это как если бы ты решил запечь торт и каждый раз добавлял по два яйца — в итоге у тебя получится не торт, а яичный омлет!

Пример из реальной жизни

Представь себе игру в футбол. Если ты начинаешь с нуля и постепенно увеличиваешь количество тренировок, то твои навыки будут расти. Но представь, что после определенного момента твои навыки начинают приближаться к максимальному уровню. Это можно описать асимптотически: твои навыки будут расти, но не бесконечно. В какой-то момент они достигнут плато — это и есть асимптотическое поведение!

Интересные факты

Знаешь ли ты, что понятие асимптоты пришло из геометрии? Греки использовали его для описания кривых и линий! А еще существует целая наука под названием "асимптотическая теория", которая изучает поведение функций в предельных случаях. Это как если бы ты изучал поведение людей на вечеринке: чем больше людей приходит, тем более предсказуемым становится их поведение — они все начинают танцевать под одну и ту же музыку!

Визуальный пример на Python

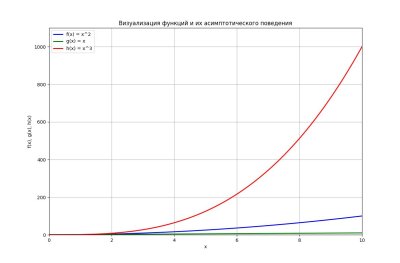
Давайте создадим более наглядный пример, который будет включать несколько функций и их асимптотическое поведение, чтобы показать, как они соотносятся друг с другом. Мы визуализируем три функции: f(x) = x² , g(x) = x и h(x) = x³ . Это поможет увидеть, как различные функции ведут себя на разных интервалах.

import numpy as np
import matplotlib.pyplot as plt

# Определяем функции
def f(x):
    return x**2

def g(x):
    return x

def h(x):
    return x**3

# Создаем массив значений x
x = np.linspace(0, 10, 1000)

# Вычисляем значения функций
y_f = f(x)
y_g = g(x)
y_h = h(x)

# Визуализация
plt.figure(figsize=(12, 8))

# График f(x) = x^2
plt.plot(x, y_f, label='f(x) = x^2', color='blue', linewidth=2)

# График g(x) = x
plt.plot(x, y_g, label='g(x) = x', color='green', linewidth=2)

# График h(x) = x^3
plt.plot(x, y_h, label='h(x) = x^3', color='red', linewidth=2)

# Добавляем горизонтальные линии для асимптотического поведения
plt.axhline(0, color='black', lw=0.5, ls='--')
plt.axvline(0, color='black', lw=0.5, ls='--')

# Настройка графика
plt.title('Визуализация функций и их асимптотического поведения')
plt.xlabel('x')
plt.ylabel('f(x), g(x), h(x)')
plt.xlim(0, 10)
plt.ylim(0, 1100)
plt.grid()
plt.legend()
plt.show()

Новые понятия

• Aсимптота: Линия, к которой функция стремится при определенных значениях аргумента.


• Aсимптотический анализ: Метод анализа поведения функций или алгоритмов при больших входных данных.


• Вертикальная асимптота: Линия, к которой функция стремится при приближении аргумента к определенному значению.


• Горизонтальная асимптота: Линия, к которой функция стремится при стремлении аргумента к бесконечности.


• Наклонная асимптота: Линия, описывающая поведение функции на бесконечности.

Так что запомни: асимптотика — это не просто скучные формулы и графики; это способ понять мир вокруг нас через призму математики. И кто знает, возможно, однажды ты станешь великим математиком или программистом и сможешь использовать эти знания для создания чего-то потрясающего! А пока просто помни: как бы ни были сложны функции, всегда можно найти их асимптоты и понять их поведение!»