Нормальные колебания

Давай погрузимся в мир нормальных колебаний! Это тема, которая не только заставляет физиков терять покой, но и может вызвать улыбку у программистов. Нормальные колебания — это то, как системы возвращаются в равновесие после возмущения. Представь себе группу людей, которые танцуют под музыку: каждый из них двигается в такт, но иногда кто-то теряет ритм. В этом случае мы наблюдаем нормальные колебания!

Что такое нормальные колебания?

Нормальные колебания — это специфические формы движения системы, при которых все её части колеблются с одинаковой частотой. Например, представь себе пружину с несколькими массами на ней. Если ты сдвинешь одну массу, все остальные начнут двигаться в унисон. Это и есть нормальные колебания!

Пример: Модель пружины

Давай рассмотрим простую модель с двумя массами и пружинами. Мы можем смоделировать эту систему с помощью Python. Для этого нам понадобятся библиотеки NumPy и Matplotlib. Вот как это можно сделать:

import numpy as np
import matplotlib.pyplot as plt

#Параметры системы

m1 = 1  # масса 1 (кг)
m2 = 1  # масса 2 (кг)
k = 10  # жесткость пружины (Н/м)

#Частота нормальных колебаний

omega = np.sqrt(k / m1)

#Время

t = np.linspace(0, 10, 100)

#Колебания

x1 = np.cos(omega * t)  # положение первой массы
x2 = np.cos(omega * t + np.pi/2)  # положение второй массы

#Построим график

plt.plot(t, x1, label='Масса 1')
plt.plot(t, x2, label='Масса 2')
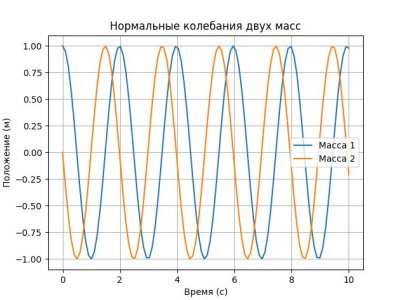
plt.title('Нормальные колебания двух масс')
plt.xlabel('Время (с)')
plt.ylabel('Положение (м)')
plt.legend()
plt.grid()
plt.show()

На графике ты увидишь, как обе массы колеблются в унисон, даже если они имеют разные фазы. Это и есть красота нормальных колебаний!

Собственные частоты

Теперь давай поговорим о собственных частотах. Каждая система имеет свои собственные частоты, которые определяются её массами и жесткостями. Чем больше масса или меньше жесткость, тем ниже собственная частота. Это похоже на то, как более тяжёлые люди могут медленнее танцевать под ту же музыку.

Пример: Собственные частоты

Представь, что у нас есть система с тремя массами и пружинами. Мы можем рассчитать собственные частоты с помощью линейной алгебры:

from scipy.linalg import eigh

#Матрица жесткости

K = np.array([[k, -k],
              [-k, k]])

#Массовая матрица

M = np.array([[m1, 0],
              [0, m2]])

#Решение собственных значений

eigenvalues, eigenvectors = eigh(K, M)

#Собственные частоты

frequencies = np.sqrt(eigenvalues)
print("Собственные частоты:", frequencies)

Здесь мы используем метод собственных значений для нахождения частот. Это полезно для сложных систем, где просто вычислить их не получится.

Влияние демпфирования

Не забудь про демпфирование! Это когда система теряет энергию из-за трения или сопротивления. Представь себе, что ты танцуешь на вечеринке, но кто-то постоянно наступает тебе на ноги. Это демпфирование! Оно влияет на амплитуду колебаний и может привести к затуханию.

Пример: Демпфированные колебания

Давай добавим демпфирование в нашу модель:

import numpy as np
import matplotlib.pyplot as plt

#Параметры системы

m1 = 1  # масса 1 (кг)
m2 = 1  # масса 2 (кг)
k = 10  # жесткость пружины (Н/м)

#Частота нормальных колебаний

omega = np.sqrt(k / m1)

#Время

t = np.linspace(0, 10, 100)

#Колебания

x1 = np.cos(omega * t)  # положение первой массы
x2 = np.cos(omega * t + np.pi/2)  # положение второй массы

b = 0.5  # коэффициент демпфирования

#Уравнение движения с демпфированием

def dampedoscillator(t):
    return np.exp(-b * t) * np.cos(omega * t)

#Построим график

dampedx1 = dampedoscillator(t)
plt.plot(t, dampedx1, label='Демпфированные колебания')
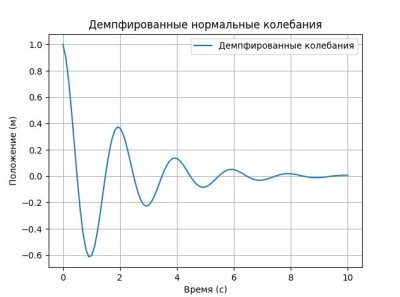
plt.title('Демпфированные нормальные колебания')
plt.xlabel('Время (с)')
plt.ylabel('Положение (м)')
plt.legend()
plt.grid()
plt.show()

На этом графике ты увидишь, как амплитуда колебаний уменьшается со временем. Это наглядно показывает эффект демпфирования.

Заключение

Нормальные колебания — это не просто скучные математические модели. Это основа многих физических процессов вокруг нас! От механических систем до электрических цепей — везде можно увидеть их влияние. Так что, когда ты в следующий раз будешь танцевать под любимую музыку, вспомни о нормальных колебаниях и о том, как они могут повлиять на твой танец!

Задания для закрепления материала

Задача 1: Колебания пружины
На пружине длиной 1 м находятся две массы: 2 кг и 3 кг. Жесткость пружины составляет 50 Н/м. Найдите частоту нормальных колебаний системы.

Задача 2: Демпфированные колебания
Система из одной массы 5 кг и пружины с жесткостью 100 Н/м испытывает демпфирование с коэффициентом 1 Н·с/m. Определите уравнение движения и постройте график колебаний.

Задача 3: Собственные частоты трехмассовой системы
В системе из трех масс (1 кг, 2 кг и 3 кг) и жесткостей пружин (100 Н/м, 150 Н/м) найдите собственные частоты. Используйте метод собственных значений для решения задачи.

Задача 4: Влияние массы на частоту
Как изменится частота нормальных колебаний системы, если массу, находящуюся на пружине с жесткостью 80 Н/м, увеличить с 2 кг до 4 кг? Обоснуйте свой ответ.

Задача 5: Устойчивость системы
Исследуйте устойчивость системы, состоящей из двух масс (1 кг и 2 кг), соединенных пружинами с жесткостями 30 Н/м и 60 Н/м. Определите, будет ли система устойчивой при малом возмущении.