Отрезок

Ты когда-нибудь задумывался, что отрезок — это не просто линия, а целый набор свойств и возможностей? Давай разберемся, что такое отрезок, как его можно измерить и какие интересные свойства у него есть.

Что такое отрезок?

Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка. Представь себе, что ты взял линейку и провел по ней карандашом, но не до конца — вот это и есть отрезок! В отличие от прямой, которая продолжается бесконечно в обе стороны, отрезок имеет свои границы. И да, он не любит, когда его растягивают!

Более формальное определение:

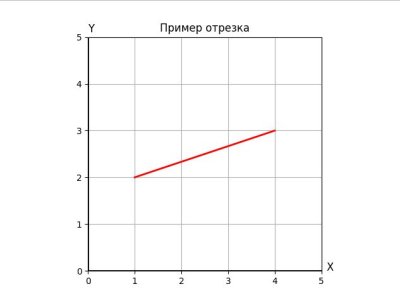
Пример отрезка на Python

import matplotlib.pyplot as plt

def draw_axes():
    # Устанавливаем пределы осей
    plt.xlim(0, 5)
    plt.ylim(0, 5)

    # Рисуем оси
    plt.axhline(0, color='black', lw=2)  # Ось X
    plt.axvline(0, color='black', lw=2)  # Ось Y

    # Подписываем оси
    plt.text(5.1, 0, 'X', fontsize=12)
    plt.text(0, 5.1, 'Y', fontsize=12)

def draw_line(x1, y1, x2, y2):
    plt.plot([x1, x2], [y1, y2], color='red', linewidth=2)  # Рисуем линию

def main():
    draw_axes()  # Рисуем координатные оси

    # Координаты точек A и B
    Ax = 1
    Ay = 2  # Точка A
    Bx = 4
    By = 3  # Точка B

    draw_line(Ax, Ay, Bx, By)  # Рисуем отрезок между A и B

    plt.grid()  # Включаем сетку
    plt.gca().set_aspect('equal', adjustable='box')  # Устанавливаем равные масштабы осей
    plt.title('Пример отрезка')  # Заголовок графика
    plt.show()  # Показываем график

if __name__ == "__main__":
    main()

Длина отрезка

Чтобы измерить длину отрезка, нам понадобятся координаты его концов. Допустим, у нас есть точки A (x₁, y₁) и B (x₂, y₂). Длину отрезка можно вычислить с помощью формулы:

length = ((x2 - x1)2 + (y2 - y1)2) ** 0.5

Эта формула основана на теореме Пифагора. Если ты забудешь, что такое теорема Пифагора, просто вспомни про треугольники и гипотенузы — и все станет на свои места!

Пример с длиной отрезка

Представь, что у нас есть точки A (1, 2) и B (4, 6). Давай посчитаем длину отрезка AB:

x1, y1 = 1, 2
x2, y2 = 4, 6
length = ((x2 - x1)2 + (y2 - y1)2) ** 0.5
print(length)  # выведет 5.0

Вуаля! Длина отрезка AB равна 5.0. Теперь ты знаешь, как измерять расстояния между точками на плоскости!

Свойства отрезков

Отрезки обладают несколькими интересными свойствами. Например, любой отрезок можно разделить на две части. Если ты проведешь линию через середину отрезка, то получишь два равных отрезка. Это свойство называется "середина отрезка".

Середина отрезка

Середина отрезка AB с координатами A (x₁, y₁) и B (x₂, y₂) находится по формуле:

midpoint_x = (x1 + x2) / 2
midpoint_y = (y1 + y2) / 2
midpoint = (midpointx, midpointy)

Если продолжить наш пример с точками A (1, 2) и B (4, 6), то середина отрезка будет:

midpoint_x = (1 + 4) / 2
midpoint_y = (2 + 6) / 2
midpoint = (midpointx, midpointy)
print(midpoint)  # выведет (2.5, 4.0)

Теперь ты знаешь, как находить середину отрезка! Она всегда будет находиться ровно посередине — как будто ждет тебя с чашкой чая.

Параллельные и перпендикулярные отрезки

Еще одно интересное свойство — это параллельность и перпендикулярность отрезков. Два отрезка называются параллельными, если они никогда не пересекаются, даже если их продолжить до бесконечности. А перпендикулярные отрезки пересекаются под углом 90 градусов. Это как два друга, которые встретились на углу улицы!

Как проверить параллельность?

Чтобы проверить, параллельны ли два отрезка AB и CD, нужно сравнить их наклоны. Наклон отрезка можно найти по формуле:

slope_AB = (y2 - y1) / (x2 - x1)
slope_CD = (y4 - y3) / (x4 - x3)
if slopeAB == slopeCD:
    print("Отрезки параллельны")
else:
    print("Отрезки не параллельны")

Перпендикулярность

Чтобы проверить перпендикулярность, нужно убедиться, что произведение их наклонов равно -1:

if slopeAB * slopeCD == -1:
    print("Отрезки перпендикулярны")
else:
    print("Отрезки не перпендикулярны")

Интересные факты о отрезках

• Отрезки могут быть использованы для создания сложных фигур, таких как треугольники и многоугольники.


• В математике существует понятие "отрезок времени" — это временной интервал между двумя событиями.


• В компьютерной графике отрезки используются для построения линий и фигур на экране.

Вот такие интересные вещи скрываются за простым понятием "отрезок". Запомни: это не просто линия между двумя точками — это целая вселенная возможностей для изучения и применения в разных областях! Теперь ты готов к новым геометрическим приключениям!

Задания для закрепления материала

Задача 1: Измерение длины отрезка
Даны точки A (3, 4) и B (7, 1). Найдите длину отрезка AB.

Задача 2: Середина отрезка
Определите середину отрезка, соединяющего точки C (2, 3) и D (8, 5).

Задача 3: Параллельные отрезки
Даны отрезки EF с концами E (1, 2) и F (5, 6) и GH с концами G (2, 3) и H (6, 7). Являются ли они параллельными?

Задача 4: Перпендикулярные отрезки
Проверьте, являются ли отрезки IJ с концами I (0, 0) и J (4, 4) и KL с концами K (0, 4) и L (4, 0) перпендикулярными.

Задача 5: Сравнение длин отрезков
Даны отрезки MN с концами M (1, 1) и N (4, 5) и OP с концами O (2, 2) и P (6, 6). Какой из отрезков длиннее?